Recently, the Flexible Radio Frequency Technology Research Center of Southeast University published an innovative study in the journal IEEE Transactions on Antennas and Propagation, developing a sub-global basis function method based on hybrid variational quantum technology for analyzing the scattering characteristics of finite periodic structures. This method can leverage quantum advantage to enhance the learning efficiency of the prediction model during the training phase and its robustness when the training sample size decreases. The related findings, titled "Hybrid Variational Quantum Algorithm Enhanced Subentire-Domain Basis Functions Method with High Learning Efficiency and Better Robustness" were published in the top international journal IEEE Transactions on Antennas and Propagation.
In the electromagnetic property analysis of large-scale finite periodic structures, the computational complexity caused by edge effects and the high time and memory consumption of traditional full-wave methods constitute major challenges in the field of electromagnetic computation. Macro-basis function methods can effectively reduce the matrix order by constructing basis functions on macrocells. Among them, the subglobal domain (SED) basis function method is widely used because it can significantly reduce unknowns according to position type and has been extended to more complex structures by combining various acceleration algorithms. However, these methods still have efficiency bottlenecks when constructing reduced matrices that include the mutual coupling between all cells. The research team previously used artificial neural networks to predict the expansion coefficients of SED basis functions and accelerated the calculation with the help of data mapping, but due to the limitations of the classical computational paradigm, the model still has insufficient learning performance.
To address this challenge, this study is the first to introduce the quantum computing paradigm into the electromagnetic analysis of large-scale finite periodic structures, proposing a hybrid variable quantum algorithm-enhanced SED basis function method (SED-HVQA). The research framework consists of two steps: first, obtaining three types of position-dependent basis functions through the SED method; second, using HVQA to model the mutual coupling relationships between units, predicting the expansion coefficients of each unit by inputting structural parameter information into three sets of trained HVQA models.
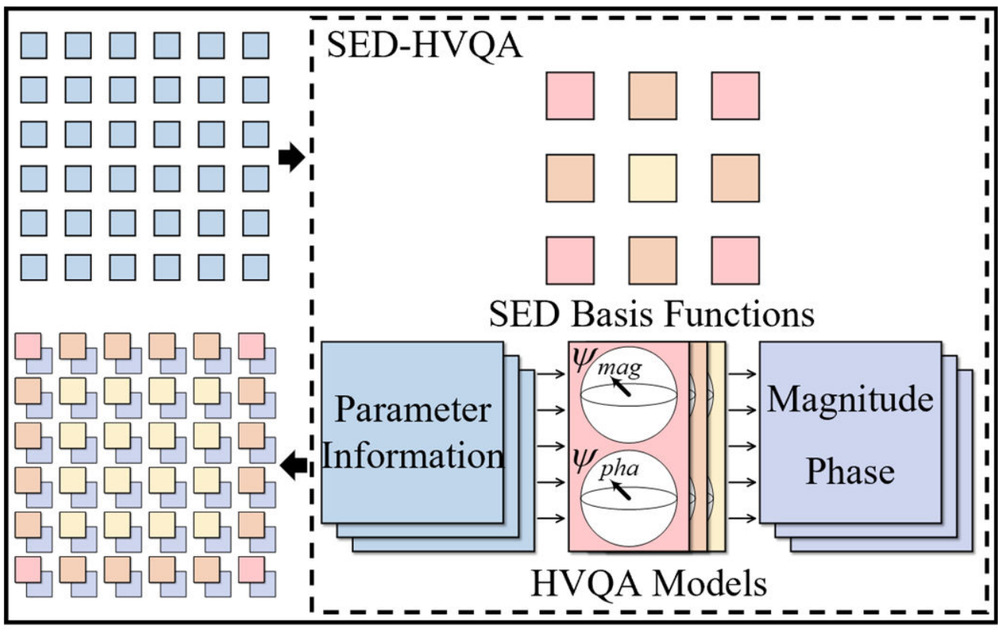
Figure 1 SED-HVQA Method Architecture Diagram
This innovative model maps parameter information to a quantum-enhanced feature space, requiring only a few qubits for encoding and evolution, far smaller than the available scale of existing mesoscale quantum devices. Finally, the research team conducted numerical experiments on a quantum simulator, demonstrating that SED-HVQA can quickly and accurately calculate the electromagnetic properties of finite-periodic structures. Especially in scenarios with strong edge effects such as corner units, the learning efficiency is improved by 27%–62%. Furthermore, when the number of training samples is reduced to 10%, the model exhibits a robustness improvement of 22%–59% across all unit types.
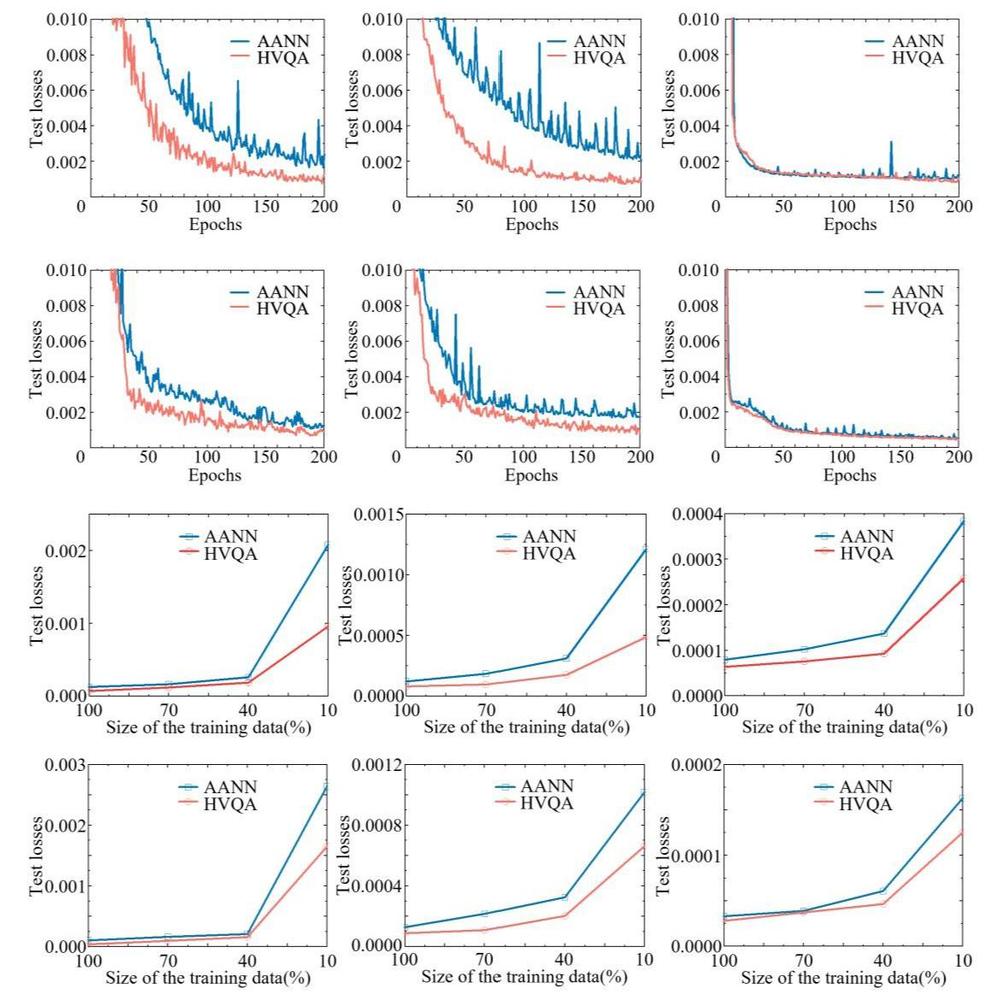
Figure 2 The learning efficiency and robustness of SED-HVQA are significantly improved compared to classical neural networks
This research, through the deep integration of the SED method and hybrid quantum algorithms, breaks through the limitations of classical neural networks in terms of learning performance and sample dependence, opens up a new path for quantum computing-assisted electromagnetic simulation, and provides an innovative solution for the efficient design of periodic structures such as frequency-selective surfaces, metasurfaces, and phased array antennas.
Paper Information
B. B. Song, T. Liu, F. X. Meng, W. Yang, and W. B. Lu, “Hybrid Variational Quantum Algorithm Enhanced Subentire-Domain Basis Functions Method with High Learning Efficiency and Better Robustness,” IEEE Trans. Antennas Propag., IEEE Early Access, Jun. 2025.
https://ieeexplore.ieee.org/document/11036609



 京公网安备 11010802027423号
京公网安备 11010802027423号